Функциональное программирование. Элементарные конструкции.

В продолжении «Лямбда-темы» в данной статье, я хочу показать основные элементарные структурные конструкции функционального программирования, которые я изучил на примере интерпретатора Scheme Online Compiler (LISP)
Как уже было отмечено ранее (в предыдущем посте), в функциональных языках, вроде бы, понятные уже нам вещи, (например, вызов функции или арифметические операции) синтаксически, выглядят иначе. В самом начале мозг программиста, недавно пересевшего на изучение «функционалки», буквально переворачивается. Настолько непривычно мыслить в новом функциональном стиле. Но, как говорится, со временем привыкаешь ко всему.
Давайте рассмотрим простейшую операцию сложения двух чисел. Казалось бы, что может быть проще. И, действительно, ничего сложного нет, однако есть нюансы, так как в «функционалке» мы оперируем только функциями.
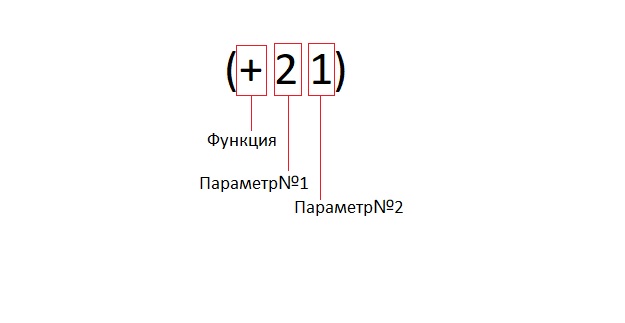
Итак, 1 + 2 = 3. Мы привыкли к такой форме записи. Но, вот как это же привычное выражение будет выглядеть на функциональном языке: (+ 1 2) – результатом этого выражения будет число 3. В первую очередь тут мы сталкиваемся с префиксной формой записи. То есть, функция “+” указывается вначале, а затем идут уже ее аргументы.
Еще одним базовым моментом является определение (define). При помощи define мы можем определить свою собственную константу или функцию.
(define my_const 7.777)
Теперь, если мы вызовем константу my_const, то интерпретатор вернет нам 7.777
Точно также мы можем определить и функцию. Давайте напишем функцию для вычисления квадрата числа и назовем ее square:
(define (square x) (* x x))
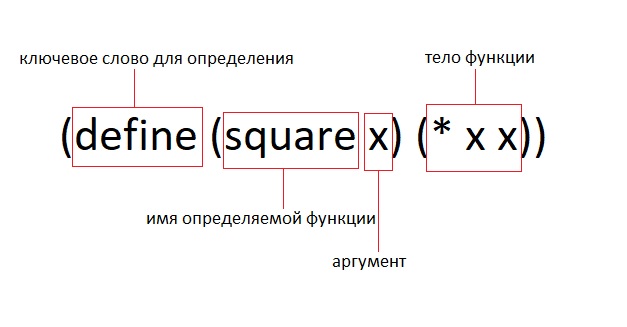
Если мы вызовем нашу функцию и передадим ей параметр 2 (square 2), то она вернет нам результат 4.
Кроме того, нам доступны и булевы выражения. А раз система способна оперировать True и False, то мы можем сделать конструкцию логического ветвления - «ифчик», проще говоря:

Более сложные логические конструкции помогают делать логические операторы AND, OR, XOR, NOT.
Еще одной базовой конструкцией, которую необходимо рассмотреть является рекурсия. Да-да, функция, которая вызывает саму себя.
Для примера рассмотрим рекуррентную реализацию функции чисел Фибоначчи - Fib(n).
Как мы знаем Fib(0) = 0, Fib(1) = 1, Fib(n-1) + Fib(n-2)
В итоге имеем следующую последовательность: 0, 1, 1, 2, 3, 5, 8, 13, 21 … n

Ну а с помощью рекурсии, точнее при помощи параметризации вызова, мы можем описать такую базовую конструкцию в языках программирования, как цикл! Да, цикл в функциональных языках реализован через рекурсию. В LISP цикл loop мы можем записать так:
(define (loop start end acc)
(if (> start end) acc (loop (+ start 1) end (+ acc start))))
Давайте запишем нашу функцию Fib(n) в итеративном стиле (при помощи цикла).
(define (fib n) (fib-iter 1 0 n))
(define (fib-iter a b count)
(if (= count 0) b (fib-iter (+ a b) a (- count 1)))))
В данном примере мы использовали внутреннее определение (функция fib-iter использована в теле функции fib, а затем только определена)
Стоит отметить, что применение рекурсии в чистом виде (не в итеративном стиле) не эффективно. Если представить графически выполнение рекуррентной функции, то получится дерево, в котором явно прослеживаются одинаковые поддеревья, результат выполнения которых не играет роли в общем вычислительном процессе. Давайте представим нашу функцию fib(n), при n = 5:
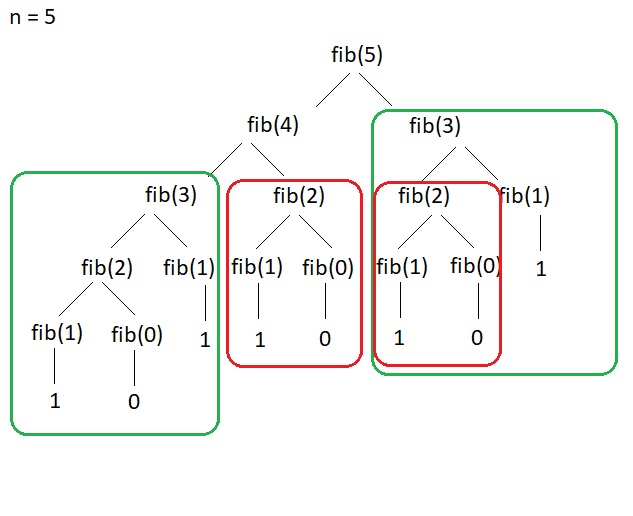 На рисунке выше, я постарался отобразить зеленым и красным цветами – одинаковые участки выполнения рекурсии.
На рисунке выше, я постарался отобразить зеленым и красным цветами – одинаковые участки выполнения рекурсии.
В данной статье я постарался показать, как при помощи элементарных комбинаций (функции, рекурсия-цикл, логические ветвления), мы можем оперировать базовыми конструкциями языка программирования.