Вселенная программирования. Вычислительные модели – основные характеристики.

В предыдущих моих постах из данной серии (раз и два), я писал о том, что глобально вселенную программирования можно разделить на микро и макро подмножества – programming in small и programming in large (ну как с экономикой). Следовательно, и круг решаемых задач разный. И вот, для того, чтобы правильно проектировать программные системы, необходимо четко выделять задачи, которые необходимо решить при помощи тех или иных наборов концепций программирования - парадигм программирования, которые уже и представляют нам конкретные языки программирования и фреймворки.
В данной статье я и хотел бы затронуть тему вычислительных моделей, которые служат основой для различных парадигм программирования. Затронуть абстрактно, исходя из той информации, которую мне удалось изучить в этом направлении.
Итак, вычислительная модель (применительно к информатике) – это набор доказанной математической теории, некий опорный вычислительный аппарат, на котором основываются те концепции, которые объединяет парадигма программирования. Например, лямбда-исчисления Алонзо Черча является математическим аппаратом - фундаментом для парадигмы функционального программирования.
Для любой парадигмы можно выделить две важнейшие ключевые характеристики:
- Степень недетерминизма (насколько он явный).
- Способность хранить значения (именованное состояние).
Недетерминизм считается явным или наблюдаемым, если мы явно видим различные результаты выполнения программы, которая имеет каждый раз одни и те же внутренние параметры при запуске. Такой характер поведения присущ, в первую очередь, для параллельного программирования (параллелизма) со свойственной ему проблемой конкуренции потоков (race condition): когда несколько частей кода могут выполняться одновременно, и нельзя по исходному тексту программы однозначно сказать, каким будет итог их работы. Потому что несколько потоков пытаются одновременно изменить состояние некоторого общего объекта, и результат зависит от промежутков времени между работой разных частей кода. Какой поток отработает последним, тот и зафиксирует итоговое состояние общего объекта. Но не всегда данный характер является крайне нежелательным, например, при моделировании систем реального мира, как раз требуется подобная парадигма с присущим явным недетерминизмом.
Способность хранить значения (именованное состояние) – это возможность сохранять последовательность значений на протяжении хода выполнения программы. В императивной парадигме это переменные. В данной характеристике важна степень выраженности именованного состояния (stateless - stateful).
Итак, если попытаться представить основные направления вычислительных моделей, и, как следствие, парадигм программирования, то мы получим некое дерево.
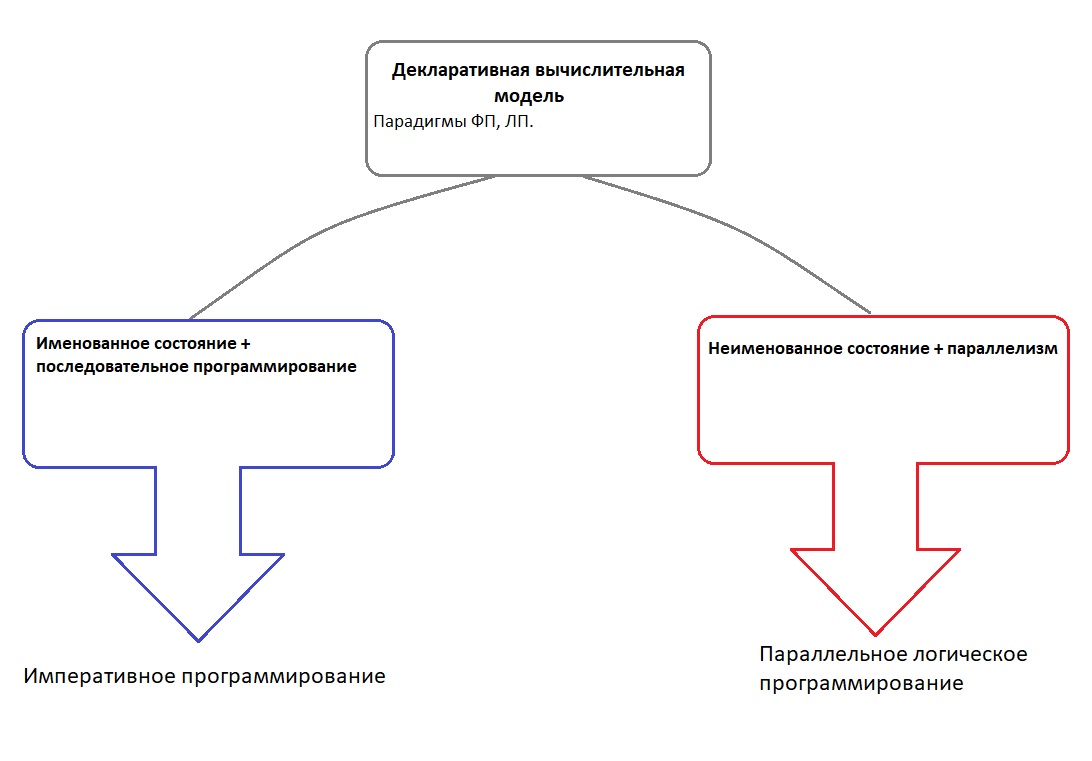
Ядро всей программистской концепции, некие глубинные принципы всего – это декларативная вычислительная модель (декларативное программирование). Если очень поверхностно описать суть, то это stateless-программирование, где не используются переменные для хранения промежуточных состояний программы, которые могут меняться с течением времени исполнения кода и, соответственно, степень именованного состояния наименее выражена. Явный представитель декларативной модели – парадигмы функционального и логического программирования. Я уже писал пару постов на тему функционального программирования более подробно (раз и два). В концепции функционального программирования мы последовательно вызываем чистые функции, подавая им на вход неизменяемые значения. Данная модель имеет явный детерминистический характер, и может быть использована для создания распределенных безопасных программных систем устойчивых к сбоям. Кроме того, данной модели свойственна параллельность (использование многопоточности – об этом отдельно поговорим позже). А значит это явная возможность эффективно использовать многоядерность современных процессоров, не упираясь в проблемы конкуренции параллельных потоков (race condition).
От данной вычислительной модели, как от корня вниз уже могут исходить ветви направлений.
Например, недетерминированная последовательная модель с более выраженной степенью именованного состояния (stateful), без параллелизма. Добавление именованного состояния даёт нам классическое императивное программирование: функции и переменные.
Другая ветвь - параллельная детерминированная модель, с неименованными состояниями (stateless), где добавление параллельности приводит к парадигме параллельного логического программирования.
Данная схема всего лишь абстрактное представление основных направлений, в терминах которых и описаны те или иные парадигмы, представителями которых являются уже конкретные языки программирования, как имплементации определенных наборов концепций.
Что же в итоге нам все это дает в реальности? А то, что искусство проектирования программных систем – это умение выбирать парадигму с оптимальным множеством концепций, точнее всего подходящим конкретному проекту. Если концепций, которые помогут достичь цели проекта, будет слишком мало, то усложнится реализация системы – мы приходим к задачам programming in small. Если таких концепций будет слишком много, то сложным станет её проектирование, -это уже круг задач programming in large.
Недетерминизм важен во всех программных системах, где взаимодействие происходит в реальном времени (например, клиент-серверные системы).
Именованные состояния важны для обеспечения модульности проекта.
Явный недетерминизм и именованные состояния - две крайние ситуации, между которыми важно уметь находить баланс при проектировании.